Linear or point-projection perspective is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper.
Perspective (graphical)
Staircase in six-point perspective
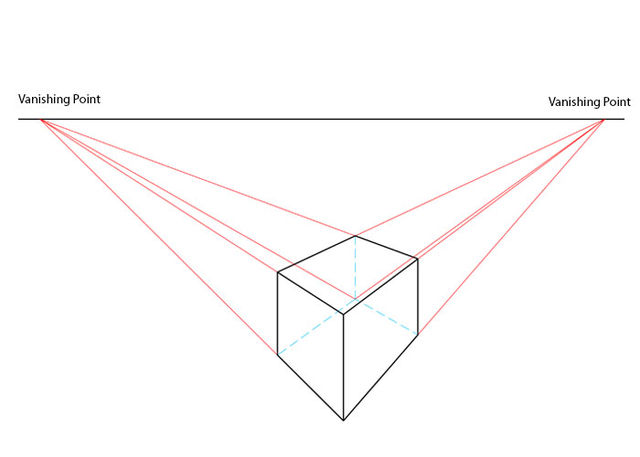
A cube drawing using two-point perspective
Chauvet cave, spatially effective grading of a group of animals through overlap (c. 31.000 BC)
A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.
Axonometric projection of a scheme displaying the relevant elements of a vertical picture plane perspective. The standing point (P.S.) is located on the ground plane π, and the point of view (P.V.) is right above it. P.P. is its projection on the picture plane α. L.O. and L.T. are the horizon and the ground lines (linea d'orizzonte and linea di terra). The bold lines s and q lie on π, and intercept α at Ts and Tq respectively. The parallel lines through P.V. (in red) intercept L.O. in the vanishing points