ʿAbd al-Raḥmān al-Ṣūfī was an Iranian astronomer. His work Kitāb ṣuwar al-kawākib, written in 964, included both textual descriptions and illustrations. The Persian polymath Al-Biruni wrote that al-Ṣūfī's work on the ecliptic was carried out in Shiraz. Al-Ṣūfī lived at the Buyid court in Isfahan.
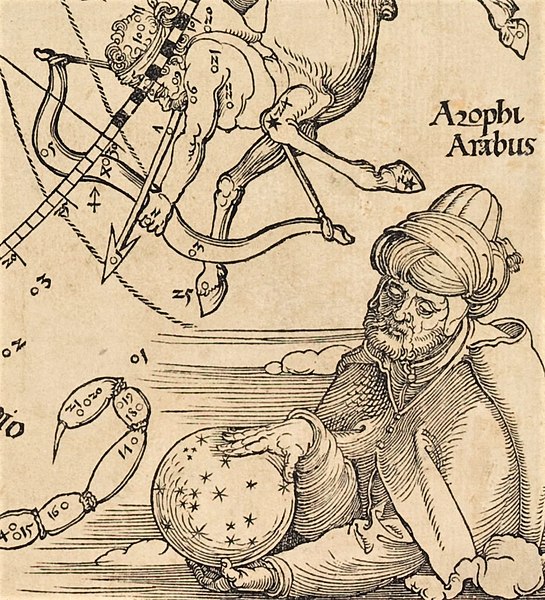
Al-Ṣūfī, as depicted in Albrecht Dürer's woodcut Imagines coeli septentrionales cum duodecim imaginibus zodiaci [The Northern Celestial Hemisphere with the Twelve Signs of the Zodiac] (1515)
“Sign of Sagittarius” by al-Sufi in his book Ṣuwar al-kawākib al-thābita, Artuqid Mardin, 1131 CE.
Sagittarius from The Depiction of Celestial Constellations
The Book of Fixed Stars is an astronomical text written by Abd al-Rahman al-Sufi (Azophi) around 964. Following the translation movement in the 9th century AD, the book was written in Arabic, the common language for scholars across the vast Islamic territories, although the author himself was Persian. It was an attempt to create a synthesis of the comprehensive star catalogue in Ptolemy’s Almagest with the indigenous Arabic astronomical traditions on the constellations. The original manuscript no longer survives as an autograph, however, the importance of tradition and the practice of diligence central to Islamic manuscript tradition have ensured the survival of the Book of Stars in later-made copies.
Two pages from an Iraqi 12th-century manuscript of the Book of Fixed Stars in the Museum of Islamic Art, Doha.
Book of Fixed Stars (Kitāb suwar al-kawākib al-ṯābita), by ‛Abd al-Rahman ibn ‛Umar al-Ṣūfī, dated 1125 CE, Baghdad (controled by the Seljuks from 1055 to 1135). Doha Museum of Islamic Art MS 2.1998. Now thought to be the oldest surviving copy.
The Great Bear. The familiar seven stars of the "Big Dipper", recorded by Ptolemy, are visible in the rump and tail, but notice they occur as a mirror-image of what we actually see because Al Sufi provided two images of each constellation, one as we see it in the night sky and one as seen here on a celestial globe. The image is from the copy in the Bodleian Library, end of 12th century CE. (Bodleian Library MS. Marsh 144).
Orion, also as a mirror image. Copy from the Bodleian Library, end of 12th century CE. (Bodleian Library MS. Marsh 144).