An aerosol is a suspension of fine solid particles or liquid droplets in air or another gas. Aerosols can be generated from natural or human causes. The term aerosol commonly refers to the mixture of particulates in air, and not to the particulate matter alone. Examples of natural aerosols are fog, mist or dust. Examples of human caused aerosols include particulate air pollutants, mist from the discharge at hydroelectric dams, irrigation mist, perfume from atomizers, smoke, dust, sprayed pesticides, and medical treatments for respiratory illnesses.
Mist and fog are aerosols
Photomicrograph made with a Scanning Electron Microscope (SEM): Fly ash particles at 2,000× magnification. Most of the particles in this aerosol are nearly spherical.
Aerosol pollution over northern India and Bangladesh
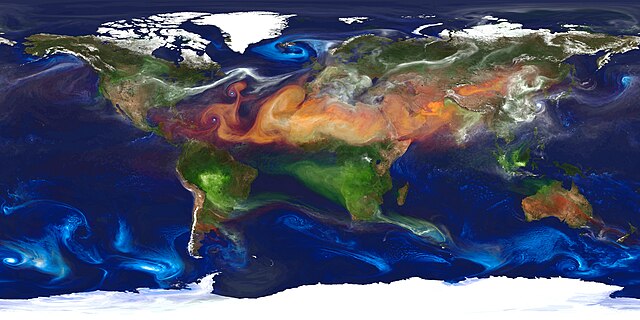
Overview of large clouds of aerosols around Earth (green: smoke, blue: salt, yellow: dust, white: sulfuric)
In chemistry, a suspension is a heterogeneous mixture of a fluid that contains solid particles sufficiently large for sedimentation. The particles may be visible to the naked eye, usually must be larger than one micrometer, and will eventually settle, although the mixture is only classified as a suspension when and while the particles have not settled out.
A suspension of flour mixed in a glass of water, showing the Tyndall effect