Arkansas is a landlocked state in the South Central region of the Southern United States. It borders Missouri to the north, Tennessee and Mississippi to the east, Louisiana to the south, Texas to the southwest, and Oklahoma to the west. Its name derives from the Osage language, and refers to their relatives, the Quapaw people. The state's diverse geography ranges from the mountainous regions of the Ozark and Ouachita Mountains, which make up the U.S. Interior Highlands, to the densely forested land in the south known as the Arkansas Timberlands, to the eastern lowlands along the Mississippi River and the Arkansas Delta.
Platform mounds were constructed frequently during the Woodland and Mississippian periods.
Arkansas statehood, 100th anniversary issue; released on June 15, 1936, on the 100th anniversary of Arkansas statehood. The old state house is depicted at center, the fort surrounding the Arkansas Post at left with the present day state capitol building at right.
Lakeport Plantation, built c. 1859
Cannons at Battle of Pea Ridge site
Missouri is a landlocked state in the Midwestern region of the United States. Ranking 21st in land area, it borders Iowa to the north, Illinois, Kentucky and Tennessee to the east, Arkansas to the south and Oklahoma, Kansas, and Nebraska to the west. In the south are the Ozarks, a forested highland, providing timber, minerals, and recreation. The Missouri River, after which the state is named, flows through the center and into the Mississippi River, which makes up the eastern border. With over six million residents, it is the 18th-most populous state of the country. The largest urban areas are St. Louis, Kansas City, Springfield, and Columbia; the capital is Jefferson City.
Missouri
The Gateway Arch in St. Louis
Fur Traders Descending the Missouri by Missouri painter George Caleb Bingham
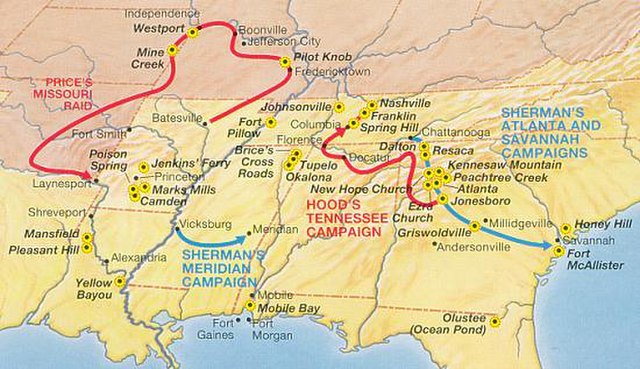
Price's Raid in the Trans-Mississippi Theater, 1864