A beam splitter or beamsplitter is an optical device that splits a beam of light into a transmitted and a reflected beam. It is a crucial part of many optical experimental and measurement systems, such as interferometers, also finding widespread application in fibre optic telecommunications.
Beam splitters
7x7 matrix using green laser and diffractive beam splitter.
Interferometry is a technique which uses the interference of superimposed waves to extract information. Interferometry typically uses electromagnetic waves and is an important investigative technique in the fields of astronomy, fiber optics, engineering metrology, optical metrology, oceanography, seismology, spectroscopy, quantum mechanics, nuclear and particle physics, plasma physics, biomolecular interactions, surface profiling, microfluidics, mechanical stress/strain measurement, velocimetry, optometry, and making holograms.
Figure 11. The VLA interferometer
ALMA is an astronomical interferometer located in Chajnantor Plateau
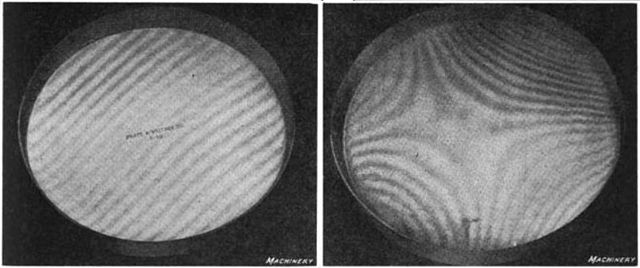
Figure 13. Optical flat interference fringes. (left) flat surface, (right) curved surface.
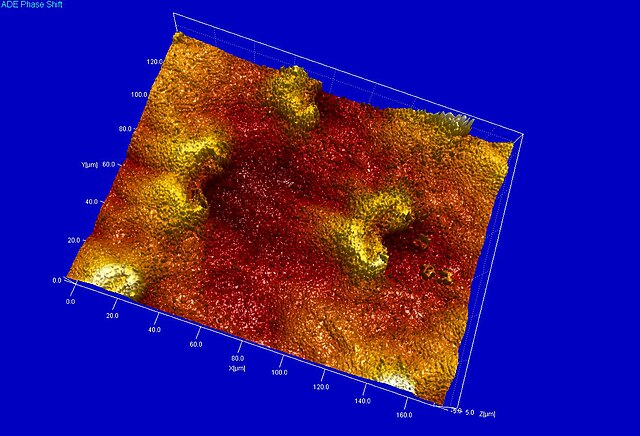
Figure 18. Lunate cells of Nepenthes khasiana visualized by Scanning White Light Interferometry (SWLI)