In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.
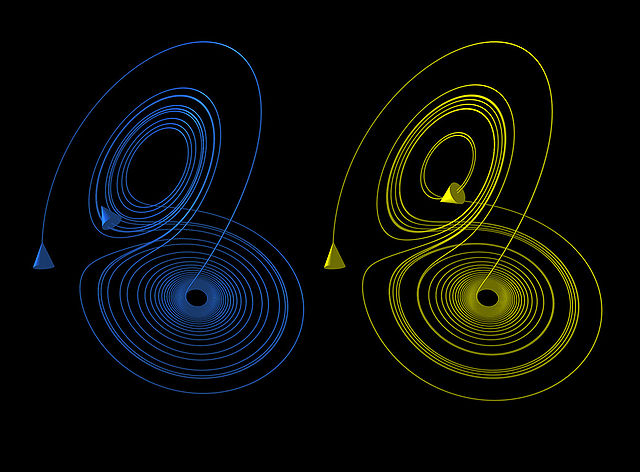
Image: Two Lorenz Orbits
Image: Lorenz Coordinates Small
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.
The Lorenz attractor displays chaotic behavior. These two plots demonstrate sensitive dependence on initial conditions within the region of phase space occupied by the attractor.
Turbulence in the tip vortex from an airplane wing. Studies of the critical point beyond which a system creates turbulence were important for chaos theory, analyzed for example by the Soviet physicist Lev Landau, who developed the Landau-Hopf theory of turbulence. David Ruelle and Floris Takens later predicted, against Landau, that fluid turbulence could develop through a strange attractor, a main concept of chaos theory.
A conus textile shell, similar in appearance to Rule 30, a cellular automaton with chaotic behaviour.