Chinese mathematics
Videos
Mathematics emerged independently in China by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numer
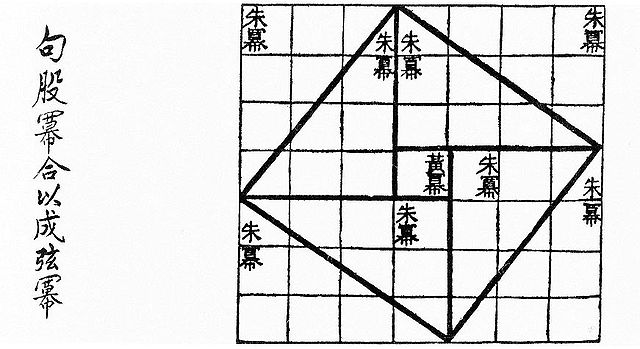
Visual proof for the (3, 4, 5) triangle as in the Zhoubi Suanjing 500–200 BCE
Liu Hui's Survey of sea island
Statue of Zu Chongzhi.
Li Ye's inscribed circle in triangle:Diagram of a round town
Pascal's triangle
Videos
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world
Chinese mathematics
…mathematics such as geometry or number theory. The Pythagorean theorem for example, has been attested to the time of the Duke of Zhou. Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal, such as the Song-era polymath Shen Kuo. One of the oldest surviving mathematical…
Pascal's version of the triangle