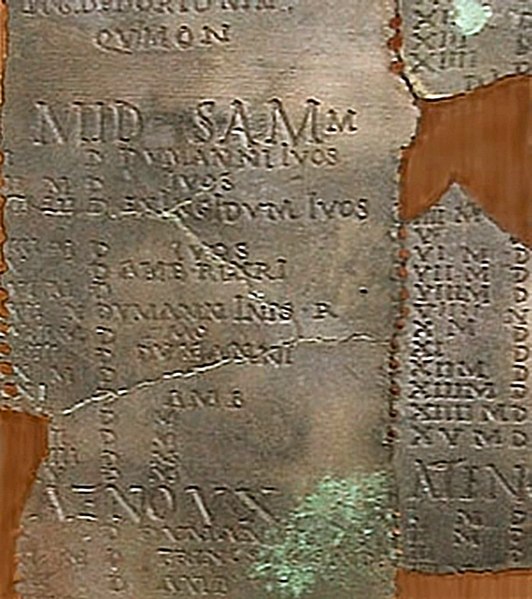The Coligny calendar is a bronze plaque with an inscribed calendar, made in Roman Gaul in the 2nd century CE. It lays out a five-year cycle of a lunisolar calendar, each year with twelve lunar months. An intercalary month is inserted before each 2.5 years. The lunar phase is tracked with exceptional precision, adjusted when necessary by a variable month, and the calendar uses the 19-year Metonic cycle to keep track of the solar year. It is the most important evidence for the reconstruction of an ancient Celtic calendar.

A lunisolar calendar is a calendar in many cultures, incorporating lunar calendars and solar calendars. The date of lunisolar calendars therefore indicates both the Moon phase and the time of the solar year, that is the position of the Sun in the Earth's sky. If the sidereal year is used instead of the solar year, then the calendar will predict the constellation near which the full moon may occur. As with all calendars which divide the year into months there is an additional requirement that the year have a whole number of months. In some case ordinary years consist of twelve months but every second or third year is an embolismic year, which adds a thirteenth intercalary, embolismic, or leap month.