Diffusion-limited aggregation
Diffusion-limited aggregation (DLA) is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles. This theory, proposed by T.A. Witten Jr. and L.M. Sander in 1981, is applicable to aggregation in any system where diffusion is the primary means of transport in the system. DLA can be observed in many systems such as electrodeposition, Hele-Shaw flow, mineral deposits, and dielectric breakdown.
A DLA cluster grown from a copper sulfate solution in an electrodeposition cell
A DLA obtained by allowing random walkers to adhere to a straight line. Different colors indicate different arrival time of the random walkers.
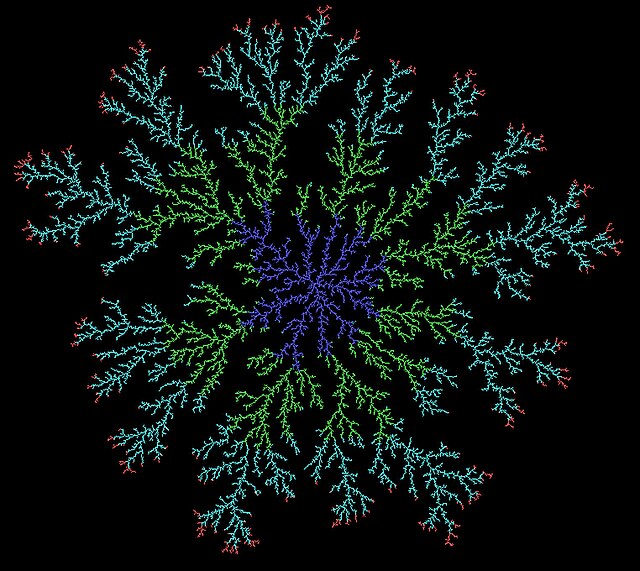
A DLA consisting of about 33,000 particles obtained by allowing random walkers to adhere to a seed at the center. Different colors indicate different arrival time of the random walkers.
High-voltage dielectric breakdown within a block of plexiglas creates a fractal pattern called a Lichtenberg figure. The branching discharges ultimately become hairlike, but are thought to extend down to the molecular level.
Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.
Diffusion furnaces used for thermal oxidation