Digital image processing
Videos
Digital image processing is the use of a digital computer to process digital images through an algorithm. As a subcategory or field of digital signal processing, digital image processing has many adva
Original lotus
Denoising picture with dilation method
Denoising picture with closing method
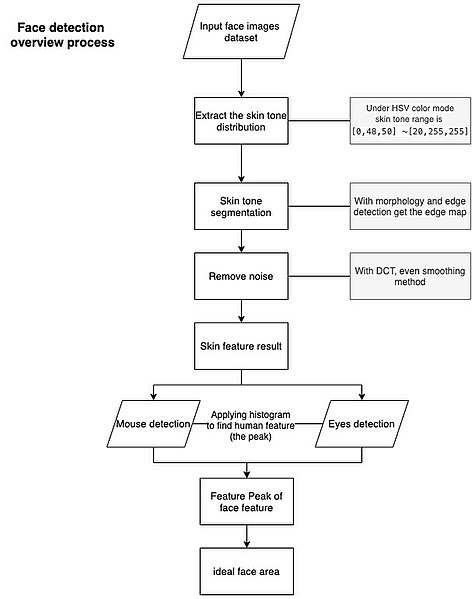
Face detection process
Image editing
Videos
Image editing encompasses the processes of altering images, whether they are digital photographs, traditional photo-chemical photographs, or illustrations. Traditional analog image editing is known as
Digital image processing
…Hidden Markov models Image editing Image restoration…
Leonardo da Vinci's Vitruvian Man overlaid with Goethe's Color Wheel using a screen layer in Adobe Photoshop. Screen layers can be helpful in graphic design and in creating multiple exposures in photography.
Leonardo da Vinci's Vitruvian Man overlaid a soft light layer Moses Harris's Color Wheel and a soft light layer of Ignaz Schiffermüller's Color Wheel. Soft light layers have a darker, more translucent look than screen layers.
Uncropped image from camera
Lily cropped from larger image