Discrete cosine transform
A discrete cosine transform (DCT) expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies. The DCT, first proposed by Nasir Ahmed in 1972, is a widely used transformation technique in signal processing and data compression. It is used in most digital media, including digital images, digital video, digital audio, digital television, digital radio, and speech coding. DCTs are also important to numerous other applications in science and engineering, such as digital signal processing, telecommunication devices, reducing network bandwidth usage, and spectral methods for the numerical solution of partial differential equations.
The four basic stages of computing 3-D DCT-II using VR DIF Algorithm.
The single butterfly stage of VR DIF algorithm.
In information theory, data compression, source coding, or bit-rate reduction is the process of encoding information using fewer bits than the original representation. Any particular compression is either lossy or lossless. Lossless compression reduces bits by identifying and eliminating statistical redundancy. No information is lost in lossless compression. Lossy compression reduces bits by removing unnecessary or less important information. Typically, a device that performs data compression is referred to as an encoder, and one that performs the reversal of the process (decompression) as a decoder.
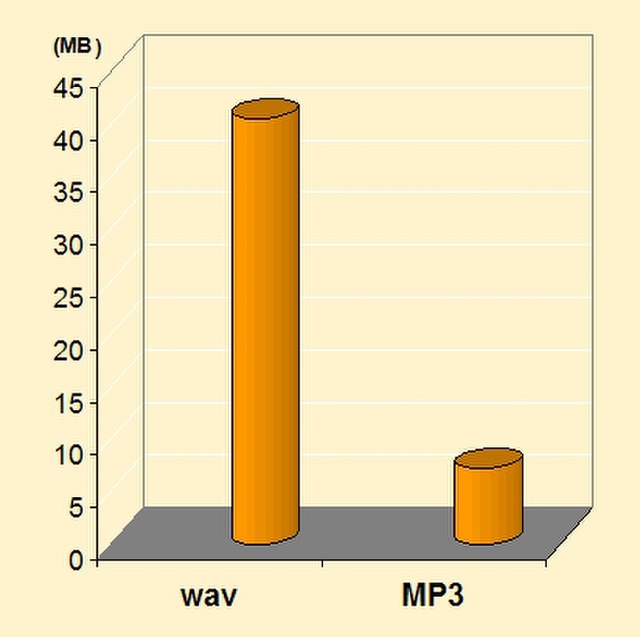
MP3, an example of a lossy file format compared to WAV.
Comparison of spectrograms of audio in an uncompressed format and several lossy formats. The lossy spectrograms show bandlimiting of higher frequencies, a common technique associated with lossy audio compression.
Solidyne 922: The world's first commercial audio bit compression sound card for PC, 1990