In electrical engineering, electrical length is a dimensionless parameter equal to the physical length of an electrical conductor such as a cable or wire, divided by the wavelength of alternating current at a given frequency traveling through the conductor. In other words, it is the length of the conductor measured in wavelengths. It can alternately be expressed as an angle, in radians or degrees, equal to the phase shift the alternating current experiences traveling through the conductor.
Reduction factor of physical length of a resonant dipole from a half-wavelength electrical length as a function of element thickness
In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmission must be taken into account. This applies especially to radio-frequency engineering because the short wavelengths mean that wave phenomena arise over very short distances. However, the theory of transmission lines was historically developed to explain phenomena on very long telegraph lines, especially submarine telegraph cables.
One of the most common types of transmission line, coaxial cable
A type of transmission line called a cage line, used for high power, low frequency applications. It functions similarly to a large coaxial cable. This example is the antenna feed line for a longwave radio transmitter in Poland, which operates at a frequency of 225 kHz and a power of 1200 kW.
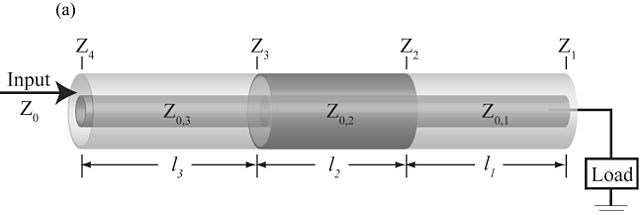
A simple example of stepped transmission line consisting of three segments
Image: Polar Smith