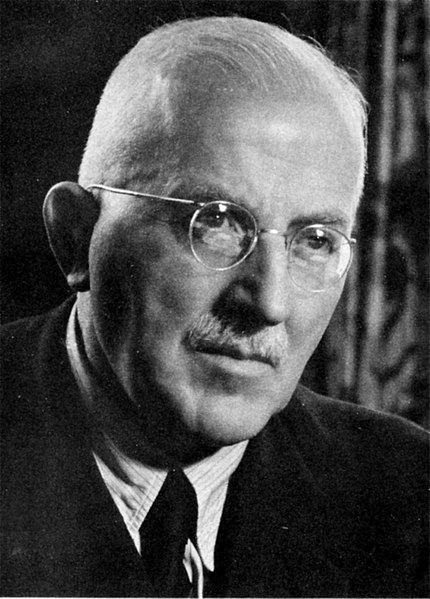Ernst Friedrich Ferdinand Zermelo was a German logician and mathematician, whose work has major implications for the foundations of mathematics. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem. Furthermore, his 1929 work on ranking chess players is the first description of a model for pairwise comparison that continues to have a profound impact on various applied fields utilizing this method.
Ernst Zermelo in the 1900s
Ernst Zermelo in Freiburg (1953)
Ernst Zermelo tombstone in Friedhof Günterstal, in Günterstal district of Freiburg im Breisgau
The University of Freiburg, officially the Albert Ludwig University of Freiburg, is a public research university located in Freiburg im Breisgau, Baden-Württemberg, Germany. The university was founded in 1457 by the Habsburg dynasty as the second university in Austrian-Habsburg territory after the University of Vienna. Today, Freiburg is the fifth-oldest university in Germany, with a long tradition of teaching the humanities, social sciences and natural sciences and technology and enjoys a high academic reputation both nationally and internationally. The university is made up of 11 faculties and attracts students from across Germany as well as from over 120 other countries. Foreign students constitute about 18.2% of total student numbers.
Portrait of Archduke Albert VI of Austria, founder of the university
Freiburg around 1900
Hermann Staudinger
The University of Freiburg in 1961