In geometry, a frustum ; is the portion of a solid that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise, it is an oblique frustum.
In a truncated cone or truncated pyramid, the truncation plane is not necessarily parallel to the cone's base, as in a frustum.
If all its edges are forced to become of the same length, then a frustum becomes a prism.
Rolo brand chocolates approximate a right circular conic frustum, although not flat on top.
Garsų Gaudyklė, Neringa, Lithuania
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a geometer. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts.
A European and an Arab practicing geometry in the 15th century
Woman teaching geometry. Illustration at the beginning of a medieval translation of Euclid's Elements, (c. 1310).
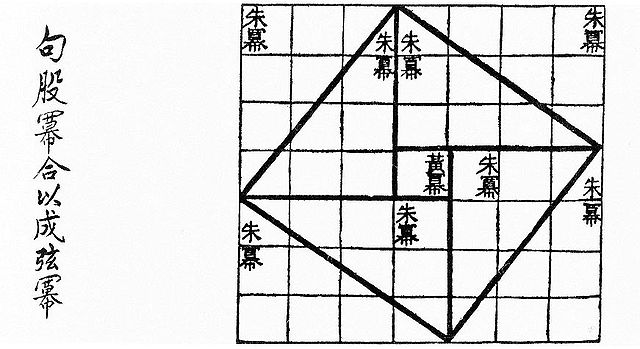
Visual checking of the Pythagorean theorem for the (3, 4, 5) triangle as in the Zhoubi Suanjing 500–200 BC. The Pythagorean theorem is a consequence of the Euclidean metric.
Quintic Calabi–Yau threefold