The history of Asia can be seen as the collective history of several distinct peripheral coastal regions such as East Asia, South Asia, Southeast Asia and the Middle East linked by the interior mass of the Eurasian steppe. See History of the Middle East and History of the Indian Subcontinent for further details on those regions.
Detail of Chinese silk from the 4th century BCE. The characteristic trade of silk through the Silk Road connected various regions from China, India, Central Asia, and the Middle East to Europe and Africa.
Some henges at Göbekli Tepe in Turkey were erected as far back as 9600 BC, predating those of Stonehenge, by over seven millennia.
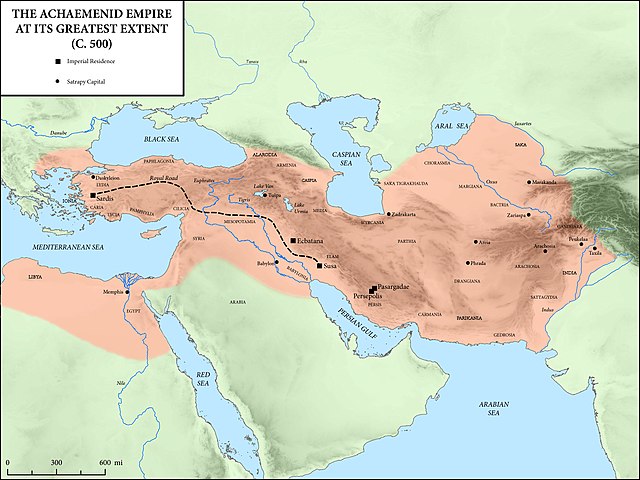
The First Persian Empire at its greatest extent, c. 500 BC
The Silk Road in Asia
The Timurid Renaissance was a historical period in Asian and Islamic history spanning the late 14th, the 15th, and the early 16th centuries. Following the gradual downturn of the Islamic Golden Age, the Timurid Empire, based in Central Asia ruled by the Timurid dynasty, witnessed the revival of arts and sciences. Its movement spread across the Muslim world. The French word renaissance means "rebirth", and defines a period as one of cultural revival. The use of the term for the description of this period has raised reservations among scholars, some of whom see it as a swan song of Timurid culture.
Illustration from Jāmī's Rose Garden of the Pious, dated 1553.
Sultan Husayn Bayqara, a patron of art, constructed multiple centers of learning.
Ulugh Beg and Ali Qushji in the observatory.
Ulugh Beg Observatory and its Madrasah has been an important centre of astronomical study in Central Asia.