Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).
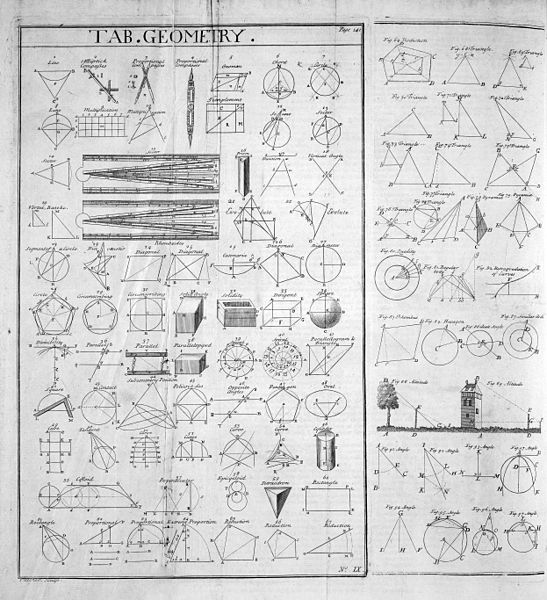
Part of the "Tab.Geometry." (Table of Geometry) from the 1728 Cyclopaedia.
Rigveda manuscript in Devanagari.
Statue of Euclid in the Oxford University Museum of Natural History.
Woman teaching geometry. Illustration at the beginning of a medieval translation of Euclid's Elements, (c. 1310)
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly from the 5th century BC to the 6th century AD, around the shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire region, from Anatolia to Italy and North Africa, but were united by Greek culture and the Greek language. The development of mathematics as a theoretical discipline and the use of deductive reasoning in proofs is an important difference between Greek mathematics and those of preceding civilizations.
Pythagoras with a tablet of ratios, detail from The School of Athens by Raphael (1509)
A fragment from Euclid's Elements (c. 300 BC), considered the most influential mathematics textbook of all time