In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Its dimension can be clarified as n-honeycomb for a honeycomb of n-dimensional space.
It is possible to fill the plane with polygons which do not meet at their corners, for example using rectangles, as in a brick wall pattern: this is not a proper tiling because corners lie part way along the edge of a neighbouring polygon. Similarly, in a proper honeycomb, there must be no edges or vertices lying part way along the face of a neighbouring cell. Interpreting each brick face as a hexagon having two interior angles of 180 degrees allows the pattern to be considered as a proper tiling. However, not all geometers accept such hexagons.
Close-packing of equal spheres
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement. Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is.
Cannonballs piled on a triangular (front) and rectangular (back) base, both FCC lattices.
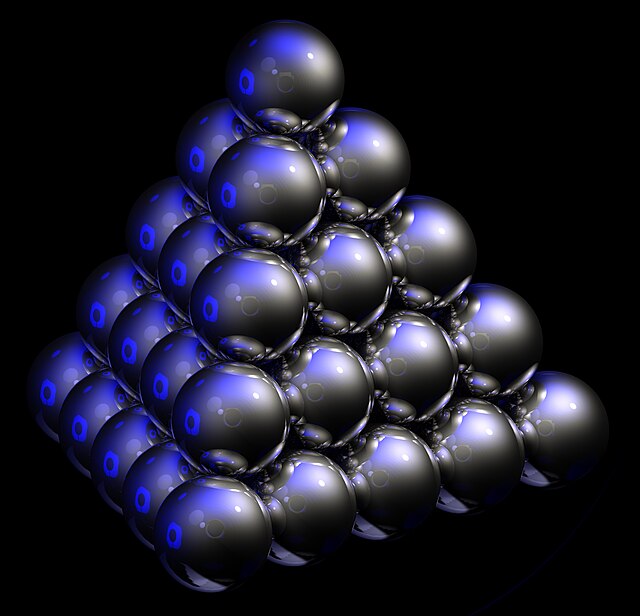
Collections of Snowballs arranged in pyramid shape. The front pyramid is hexagonal close-packed and rear is face-centered cubic.
Image: Hexagonal close packed unit cell
Image: Close packed spheres, with umbrella light & camerea