Kumyk language
Videos
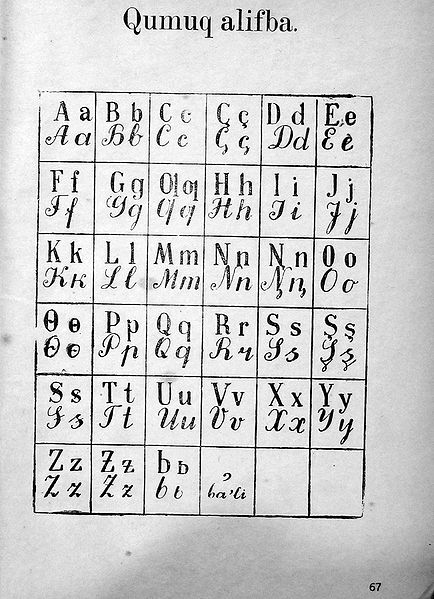
Kumyk is a Turkic language spoken by about 520,000 people, mainly by the Kumyks, in the Dagestan, North Ossetia and Chechen republics of the Russian Federation. Until the 20th century Kumyk was the li
Kumyk alphabet from newly introduced Latin school book (1935).
Turkic languages
Videos
The Turkic languages are a language family of more than 35 documented languages spoken by the Turkic peoples of Eurasia, from Southeastern Europe and Eastern Europe to Central Asia, East Asia, North A
Kumyk language
…Kumyk (къумукъ тил, qumuq til, قوموق تیل) is a Turkic language spoken by about 520,000 people, mainly by the Kumyks, in the Dagestan, North Ossetia and Chechen republics of the Russian Federation. Until the 20th…
Old Turkic Kul-chur inscription with the Old Turkic alphabet (c. 8th century). Töv Province, Mongolia
The 9th-century Irk Bitig ("Book of Divination") from Dunhuang, written in Old Uyghur language with the Orkhon script, is an important literary source for early Turko-Mongol mythology.
Yuan dynasty Buddhist inscription written in Old Uyghur language with Old Uyghur alphabet on the east wall of the Cloud Platform at Juyong Pass