Multiplication table
Videos
Page
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system.
The Tsinghua Bamboo Slips, Chinese Warring States era decimal multiplication table of 305 BC
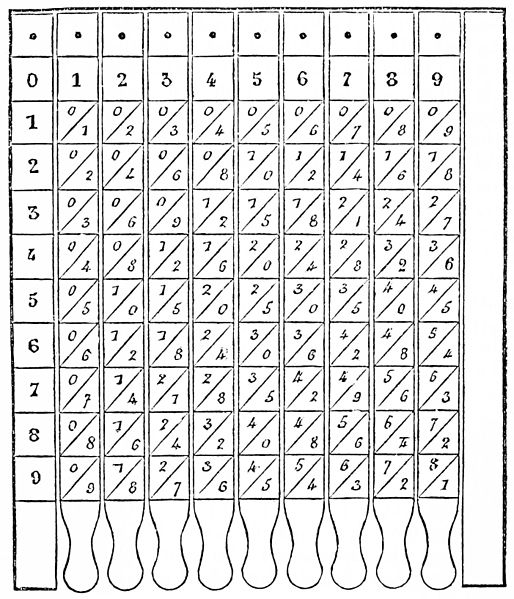
"Table of Pythagoras" on Napier's bones
Mathematical table
Videos
Page
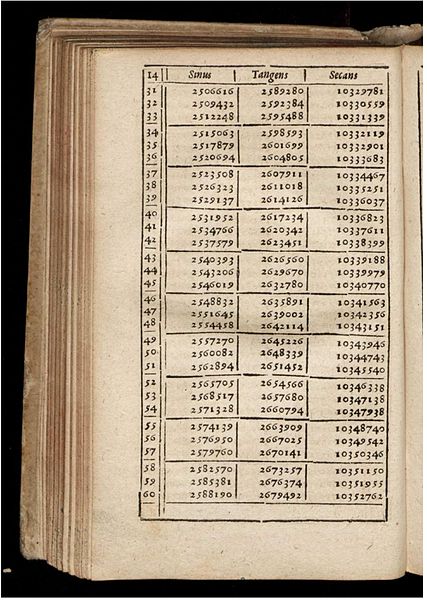
Mathematical tables are lists of numbers showing the results of a calculation with varying arguments. Trigonometric tables were used in ancient Greece and India for applications to astronomy and celestial navigation, and continued to be widely used until electronic calculators became cheap and plentiful in the 1970s, in order to simplify and drastically speed up computation. Tables of logarithms and trigonometric functions were common in math and science textbooks, and specialized tables were published for numerous applications.
These mathematical tables from 1925 were distributed by the College Entrance Examination Board to students taking the mathematics portions of the tests
A page from Henry Briggs' 1617 Logarithmorum Chilias Prima showing the base-10 (common) logarithm of the integers 0 to 67 to fourteen decimal places.
Part of a 20th-century table of common logarithms in the reference book Abramowitz and Stegun.
Image: Bernegger Manuale 136