Network topology is the arrangement of the elements of a communication network. Network topology can be used to define or describe the arrangement of various types of telecommunication networks, including command and control radio networks, industrial fieldbusses and computer networks.
Fiber-optic cables are used to transmit light from one computer/network node to another.
Personal computers are very often connected to networks using wireless links.
An ATM network interface in the form of an accessory card. A lot of network interfaces are built-in.
A typical home or small office router showing the ADSL telephone line and Ethernet network cable connections
A computer network is a set of computers sharing resources located on or provided by network nodes. Computers use common communication protocols over digital interconnections to communicate with each other. These interconnections are made up of telecommunication network technologies based on physically wired, optical, and wireless radio-frequency methods that may be arranged in a variety of network topologies.
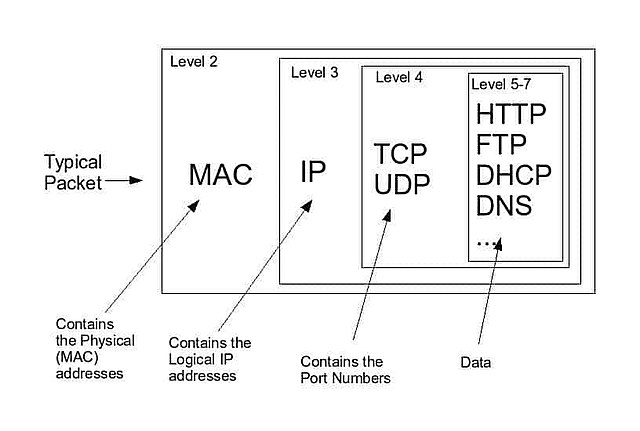
Network Packet
Fiber-optic cables are used to transmit light from one computer/network node to another.
Computers are very often connected to networks using wireless links.
An ATM network interface in the form of an accessory card. A lot of network interfaces are built-in.