In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy.
Plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50000 years. The arrows indicate the different scales used, as the eccentricities of Mercury and Mars are much greater than those of Venus and Earth. The 0 point on this plot is the year 2007.
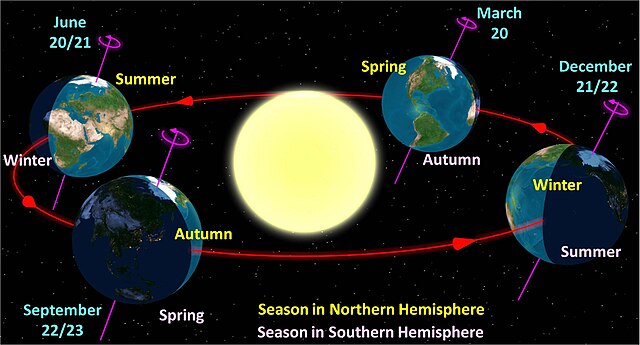
Earth orbits the Sun at an average distance of 149.60 million km in a counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes 365.256 days, during which time Earth has traveled 940 million km. Ignoring the influence of other Solar System bodies, Earth's orbit, also known as Earth's revolution, is an ellipse with the Earth-Sun barycenter as one focus with a current eccentricity of 0.0167. Since this value is close to zero, the center of the orbit is relatively close to the center of the Sun.
Earth at seasonal points in its orbit (not to scale)
Heliocentric Solar System
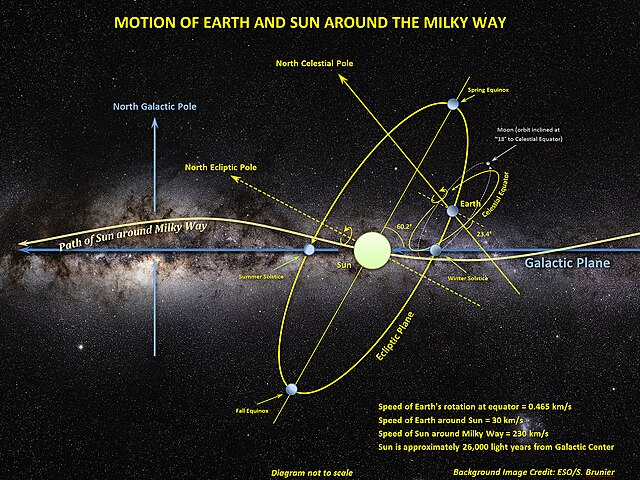
The orientation of the motion of Earth, Moon and the Sun