Ireland, also known as the Republic of Ireland, is a country in north-western Europe consisting of 26 of the 32 counties of the island of Ireland. The capital and largest city is Dublin, on the eastern side of the island. Around 2.1 million of the country's population of 5.15 million people reside in the Greater Dublin Area. The sovereign state shares its only land border with Northern Ireland, which is part of the United Kingdom. It is otherwise surrounded by the Atlantic Ocean, with the Celtic Sea to the south, St George's Channel to the south-east, and the Irish Sea to the east. It is a unitary, parliamentary republic. The legislature, the Oireachtas, consists of a lower house, Dáil Éireann; an upper house, Seanad Éireann; and an elected president who serves as the largely ceremonial head of state, but with some important powers and duties. The head of government is the Taoiseach, who is elected by the Dáil and appointed by the President, who appoints other government ministers.

The Irish Parliamentary Party was formed in 1882 by Charles Stewart Parnell (1846–1891). Charles Stewart Parnell addressing a meeting.
Damage in Dublin city centre following the 1916 Easter Rising
Leinster House , Dublin. In 1922 a new parliament called the Oireachtas was established, of which Dáil Éireann became the lower house.
Éamon de Valera, Irish political leader, pictured outside Ennis Courthouse in 1917. He would later be involved in introducing the 1937 Constitution of Ireland.
Irish, also known as Irish Gaelic or simply Gaelic, is a Goidelic language of the Insular Celtic branch of the Celtic language group, which is a part of the Indo-European language family. Irish is indigenous to the island of Ireland and was the population's first language until the 19th century, when English gradually became dominant, particularly in the last decades of the century.
Today, Irish is still commonly spoken as a first language in areas of Ireland collectively known as the Gaeltacht, in which only 2% of Ireland's population lived in 2022.
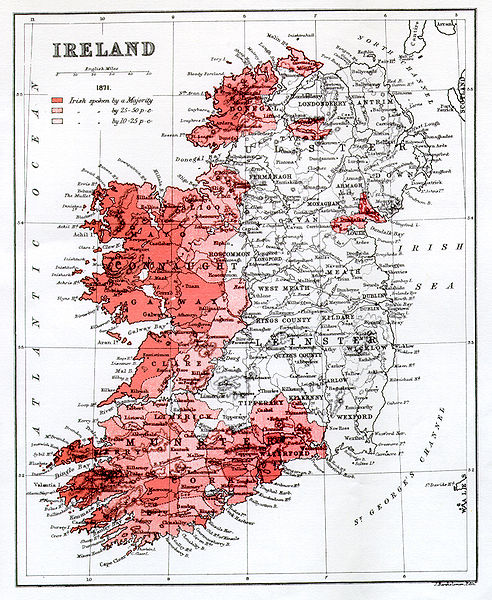
The distribution of the Irish language in 1871
Bilingual sign in Grafton Street, Dublin
Bilingual road signs in Creggs, County Galway
Dublin airport sign in both English and Irish languages