Rideau Hall is the official residence in Ottawa of both the governor general of Canada and the Canadian monarch. It stands in Canada's capital on a 36-hectare (88-acre) estate at 1 Sussex Drive, with the main building consisting of approximately 175 rooms across 9,500 square metres (102,000 sq ft), and 27 outbuildings around the grounds. Rideau Hall's site lies outside the centre of Ottawa. It is one of two official vice-regal residences maintained by the federal Crown, the other being the Citadelle of Quebec.
Main façade of Government House
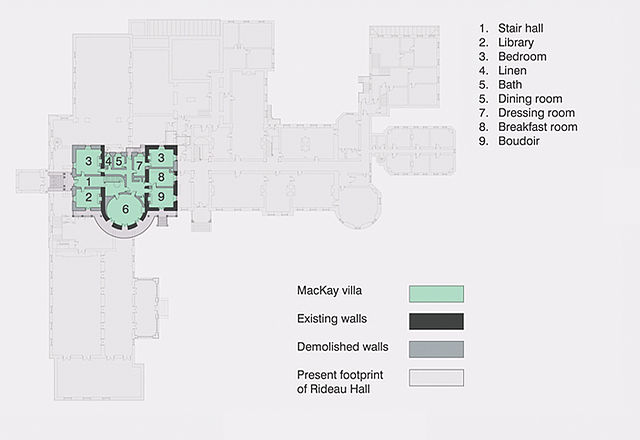
Floor plan of the original McKay villa superimposed over the present day footprint of Rideau Hall. The building was significantly expanded after its acquisition by the Crown.
Costume ball at Rideau Hall, hosted by Governor General Lord Dufferin at Rideau Hall, 1876
A May Day garden party at Rideau Hall, 1898
An official residence is a residence designated by an authority and assigned to an official, and may not always be the same place where the office holder conducts their official functions or lives.
Casa Rosada, Buenos Aires
The Government House, Yerevan
Government House, Melbourne
Hofburg Neue Burg section, seen from Heldenplatz.