Space group
Videos
In mathematics, physics and chemistry, a space group is the symmetry group of a repeating pattern in space, usually in three dimensions. The elements of a space group are the rigid transformations of
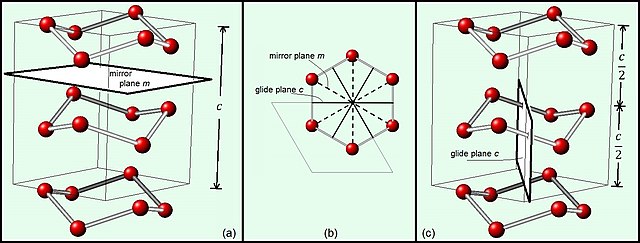
The space group of hexagonal .mw-parser-output .template-chem2-su{display:inline-block;font-size:80%;line-height:1;vertical-align:-0.35em}.mw-parser-output .template-chem2-su>span{display:block;text-align:left}.mw-parser-output sub.template-chem2-sub{font-size:80%;vertical-align:-0.35em}.mw-parser-output sup.template-chem2-sup{font-size:80%;vertical-align:0.65em}H2O ice is P63/mmc. The first m indicates the mirror plane perpendicular to the c-axis (a), the second
Wallpaper group
Videos
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, e
Space group
…of the pattern that leave it unchanged. Usually the term is applied to groups that repeat in all three dimensions, but the line groups and the wallpaper groups also apply, or can apply, to three-dimensional arrangements. The space groups that repeat in all three dimensions are classified into 219 distinct…
Example A: Cloth, Tahiti
Example B: Ornamental painting, Nineveh, Assyria
Example C: Painted porcelain, China
Medieval wall diapering