A spectral line is a weaker or stronger region in an otherwise uniform and continuous spectrum. It may result from emission or absorption of light in a narrow frequency range, compared with the nearby frequencies. Spectral lines are often used to identify atoms and molecules. These "fingerprints" can be compared to the previously collected ones of atoms and molecules, and are thus used to identify the atomic and molecular components of stars and planets, which would otherwise be impossible.
Continuous spectrum of an incandescent lamp (mid) and discrete spectrum lines of a fluorescent lamp (bottom)
Spectrum (physical sciences)
In the physical sciences, the term spectrum was introduced first into optics by Isaac Newton in the 17th century, referring to the range of colors observed when white light was dispersed through a prism.
Soon the term referred to a plot of light intensity or power as a function of frequency or wavelength, also known as a spectral density plot.
Acoustic spectrogram of the words "Oh, no!" said by a young girl, showing how the discrete spectrum of the sound (bright orange lines) changes with time (the horizontal axis)
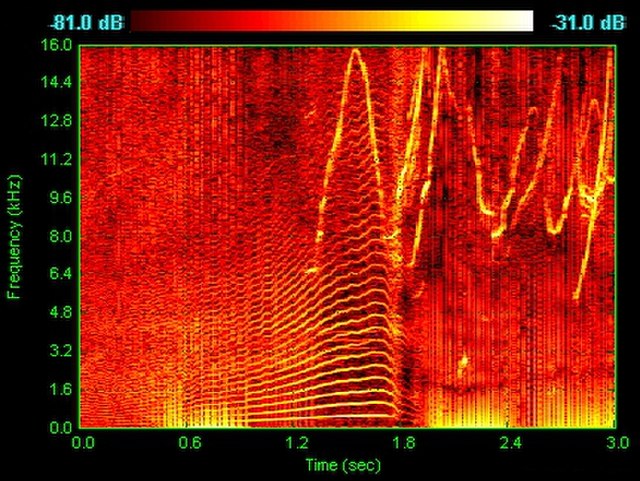
Spectrogram of dolphin vocalizations
Continuous spectrum of an incandescent lamp (mid) and discrete spectrum lines of a fluorescent lamp (bottom)