A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
An image of one of the most accurate human-made spheres, as it refracts the image of Einstein in the background. This sphere was a fused quartz gyroscope for the Gravity Probe B experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10 nm) of thickness. It was announced on 1 July 2008 that Australian scientists had created even more nearly perfect spheres, accurate to 0.3 nm, as part of an international hunt to find a new global standard kilogram.
Deck of playing cards illustrating engineering instruments, England, 1702. King of spades: Spheres
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a geometer. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts.
A European and an Arab practicing geometry in the 15th century
Woman teaching geometry. Illustration at the beginning of a medieval translation of Euclid's Elements, (c. 1310).
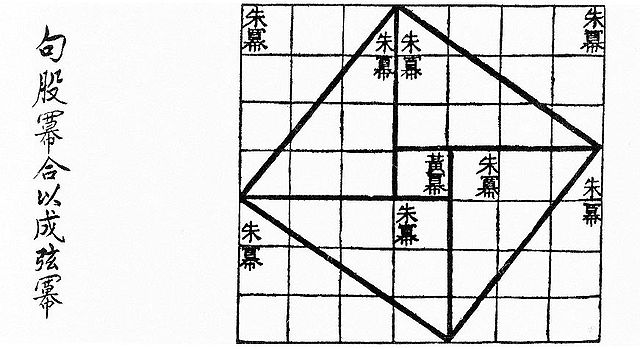
Visual checking of the Pythagorean theorem for the (3, 4, 5) triangle as in the Zhoubi Suanjing 500–200 BC. The Pythagorean theorem is a consequence of the Euclidean metric.
Quintic Calabi–Yau threefold