Thermodynamics
Videos
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these qua
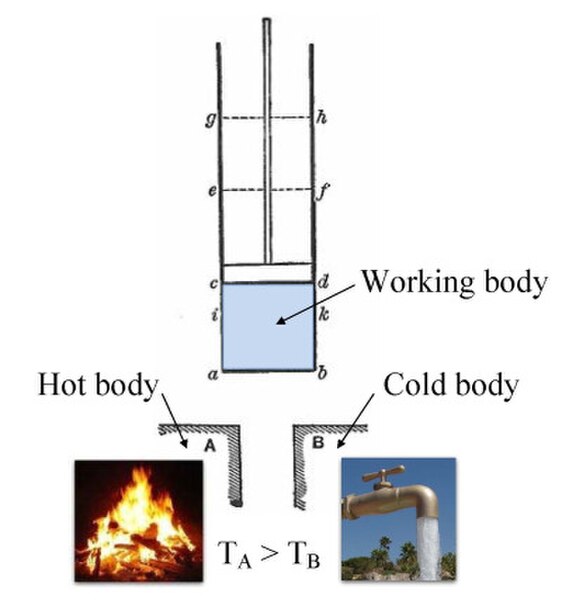
Annotated color version of the original 1824 Carnot heat engine showing the hot body (boiler), working body (system, steam), and cold body (water), the letters labeled according to the stopping points in Carnot cycle
Opening a bottle of sparkling wine (high-speed photography). The sudden drop of pressure causes a huge drop of temperature. The moisture in the air freezes, creating a smoke of tiny ice crystals.
Physics
Videos
Physics is the scientific study of matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. It is one of the most fundamental
Thermodynamics
…Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior…
Ancient Egyptian astronomy is evident in monuments like the ceiling of Senemut's tomb from the Eighteenth Dynasty of Egypt.
Aristotle (384–322 BCE)
Ibn al-Haytham (c. 965 – c. 1040) wrote of his camera obscura experiments in the Book of Optics.
Galileo Galilei (1564–1642) related mathematics, theoretical physics, and experimental physics