Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units or by various imperial or US customary units. The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid that the container could hold, rather than the amount of space the container itself displaces.
By metonymy, the term "volume" sometimes is used to refer to the corresponding region.
A measuring cup can be used to measure volumes of liquids. This cup measures volume in units of cups, fluid ounces, and millilitres.
6 volumetric measures from the mens ponderia in Pompeii, an ancient municipal institution for the control of weights and measures
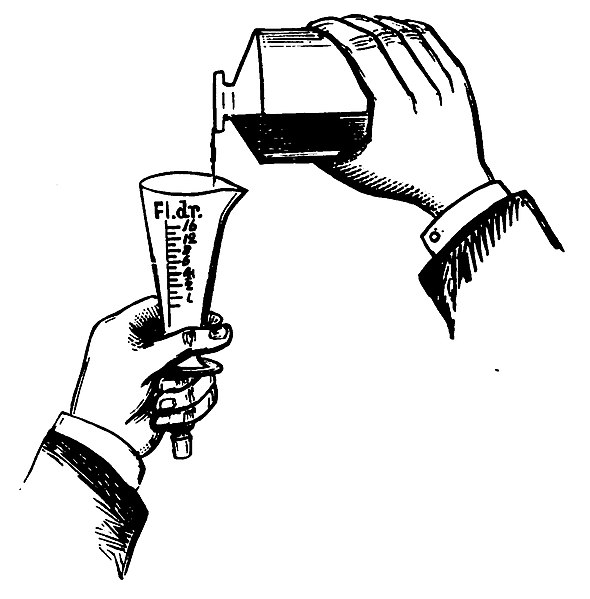
Diagram showing how to measure volume using a graduated cylinder with fluid dram markings, 1926
The litre or liter is a metric unit of volume. It is equal to 1 cubic decimetre (dm3), 1000 cubic centimetres (cm3) or 0.001 cubic metres (m3). A cubic decimetre occupies a volume of 10 cm × 10 cm × 10 cm and is thus equal to one-thousandth of a cubic metre.
One-litre beer mugs (German: Maßkrüge) at the 2006 Oktoberfest in Germany
Shot glasses with centilitre fill line graduations. "ARC" is the maker's (Arc International) certification of accuracy.