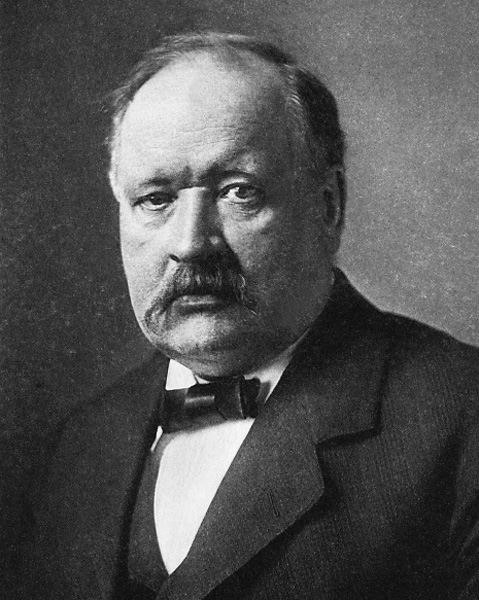In the Arrhenius model of reaction rates, activation energy is the minimum amount of energy that must be available to reactants for a chemical reaction to occur. The activation energy (Ea) of a reaction is measured in kilojoules per mole (kJ/mol) or kilocalories per mole (kcal/mol). Activation energy can be thought of as the magnitude of the potential barrier (sometimes called the energy barrier) separating minima of the potential energy surface pertaining to the initial and final thermodynamic state. For a chemical reaction to proceed at a reasonable rate, the temperature of the system should be high enough such that there exists an appreciable number of molecules with translational energy equal to or greater than the activation energy. The term "activation energy" was introduced in 1889 by the Swedish scientist Svante Arrhenius.

The sparks created by striking steel against a piece of flint provide the activation energy to initiate combustion in this Bunsen burner. The blue flame sustains itself after the sparks stop because the continued combustion of the flame is now energetically favorable.
Svante August Arrhenius was a Swedish scientist. Originally a physicist, but often referred to as a chemist, Arrhenius was one of the founders of the science of physical chemistry. He received the Nobel Prize for Chemistry in 1903, becoming the first Swedish Nobel laureate. In 1905, he became the director of the Nobel Institute, where he remained until his death.
Svante Arrhenius around 1910
Lehrbuch der kosmischen Physik, 1903
Arrhenius family grave in Uppsala
This 1902 article attributes to Arrhenius a theory that coal combustion could cause a degree of global warming eventually leading to human extinction.