Cartesian coordinate system
Videos
In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the poin
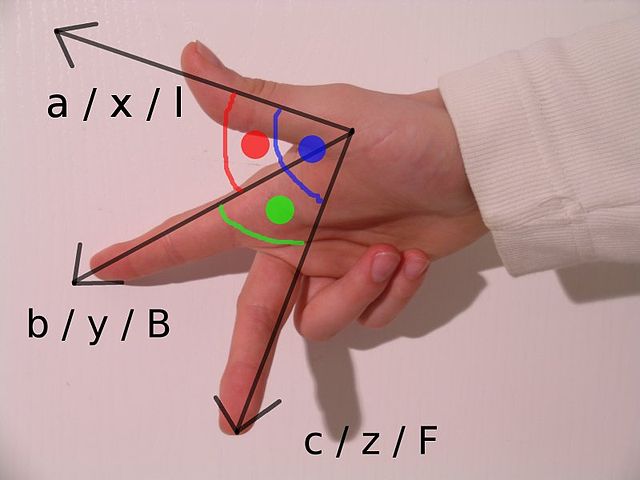
The right-hand rule
3D Cartesian coordinate handedness
René Descartes
Videos
René Descartes was a French polymath, active across philosophy, including metaphysics, epistemology, ethics, and the philosophy of science; theology; mathematics, in which he connected the previously
Cartesian coordinate system
…dimension n. These coordinates are the signed distances from the point to n mutually perpendicular fixed hyperplanes. Cartesian coordinates are named for René Descartes, whose invention thereof in the 17th century revolutionized mathematics by allowing the expression of problems of geometry in terms of algebra and…
Portrait after Frans Hals
Descartes was born in La Haye en Touraine.
Portrait of René Descartes by Jan Baptist Weenix, 1647–1649
Portrait of René Descartes by Pieter Nason (1647)