In mathematics, a curve is an object similar to a line, but that does not have to be straight.
Megalithic art from Newgrange showing an early interest in curves
A dragon curve with a positive area
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline.
This is the Ulam spiral, which illustrates the distribution of prime numbers. The dark diagonal lines in the spiral hint at the hypothesized approximate independence between being prime and being a value of a quadratic polynomial, a conjecture now known as Hardy and Littlewood's Conjecture F.
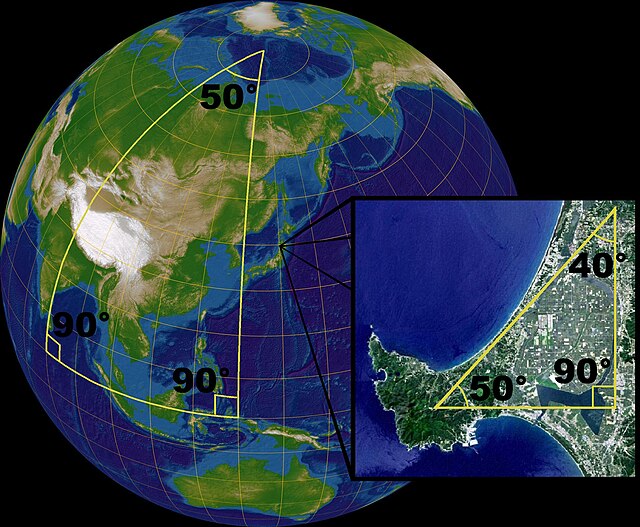
On the surface of a sphere, Euclidean geometry only applies as a local approximation. For larger scales the sum of the angles of a triangle is not equal to 180°.
The Babylonian mathematical tablet Plimpton 322, dated to 1800 BC
A page from al-Khwārizmī's Algebra