External ballistics or exterior ballistics is the part of ballistics that deals with the behavior of a projectile in flight. The projectile may be powered or un-powered, guided or unguided, spin or fin stabilized, flying through an atmosphere or in the vacuum of space, but most certainly flying under the influence of a gravitational field.
Typical trajectory graph for a M4 carbine and M16A2 rifle using identical M855 cartridges with identical projectiles. Though both trajectories have an identical 25 m near zero, the difference in muzzle velocity of the projectiles gradually causes a significant difference in trajectory and far zero. The 0 inch axis represents the line of sight or horizontal sighting plane.
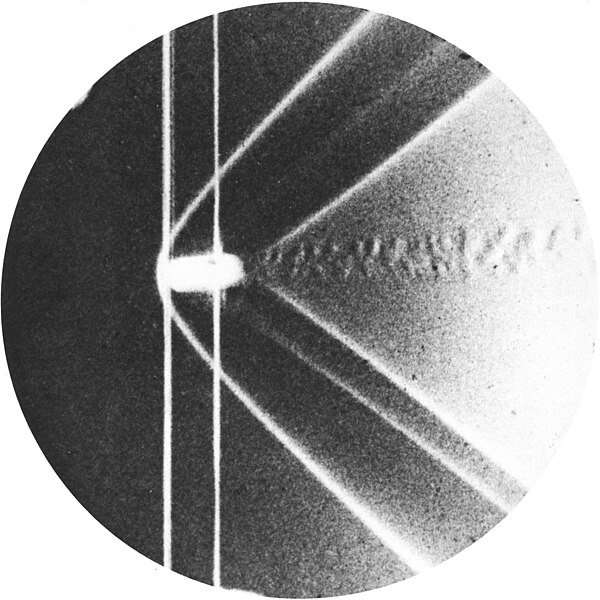
Schlieren photo/Shadowgraph of the detached shock or bow shockwave around a bullet in supersonic flight, published by Ernst Mach in 1888.
Left German 7.9 mm s.S. (FMJ) and right S.m.E. ammunition beside their boat-tailed projectiles with cannelures
Ballistics is the field of mechanics concerned with the launching, flight behaviour and impact effects of projectiles, especially ranged weapon munitions such as bullets, unguided bombs, rockets or the like; the science or art of designing and accelerating projectiles so as to achieve a desired performance.
Gaetano Marzagaglia, Del calcolo balistico, 1748
Baseball throws can exceed 100 mph
Catapult 1 Mercato San Severino
USS Iowa (BB-61) fires a full broadside, 1984.