The geoid is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents. According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century.
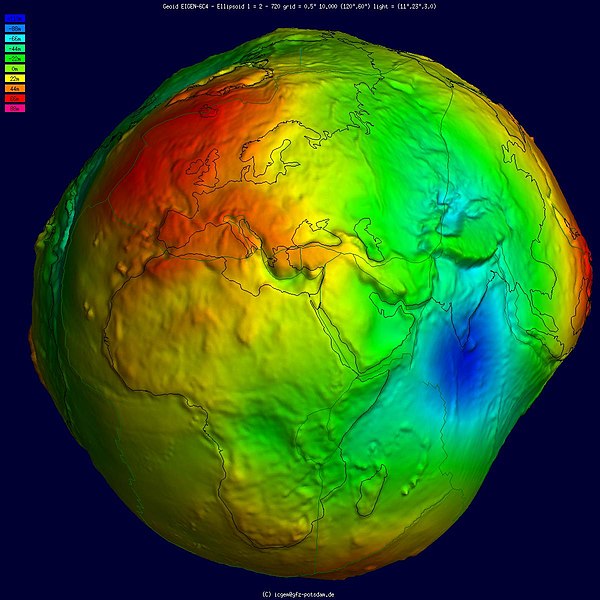
Geoid undulation in pseudocolor, shaded relief and vertical exaggeration (10000 vertical scaling factor).
Geoid undulation in pseudocolor, without vertical exaggeration.
Three-dimensional visualization of gravity anomalies in units of Gal., using pseudo color and shaded relief.
The gravity of Earth, denoted by g, is the net acceleration that is imparted to objects due to the combined effect of gravitation and the centrifugal force .
It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm .
Earth's gravity measured by NASA GRACE mission, showing deviations from the theoretical gravity of an idealized, smooth Earth, the so-called Earth ellipsoid. Red shows the areas where gravity is stronger than the smooth, standard value, and blue reveals areas where gravity is weaker (Animated version).
Earth's radial density distribution according to the Preliminary Reference Earth Model (PREM).
A plumb bob determines the local vertical direction