Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther they are, the faster they are moving away from Earth. The velocity of the galaxies has been determined by their redshift, a shift of the light they emit toward the red end of the visible spectrum. The discovery of Hubble's law is attributed to Edwin Hubble's work published in 1929.
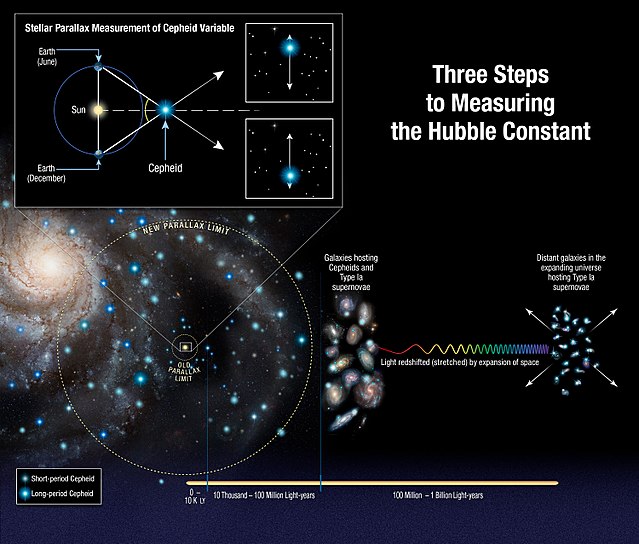
Three steps to the Hubble constant
Fit of redshift velocities to Hubble's law. Various estimates for the Hubble constant exist. The HST Key H0 Group fitted type Ia supernovae for redshifts between 0.01 and 0.1 to find that H0 = 71 ± 2 (statistical) ± 6 (systematic) km⋅s−1⋅Mpc−1, while Sandage et al. find H0 = 62.3 ± 1.3 (statistical) ± 5 (systematic) km⋅s−1⋅Mpc−1.
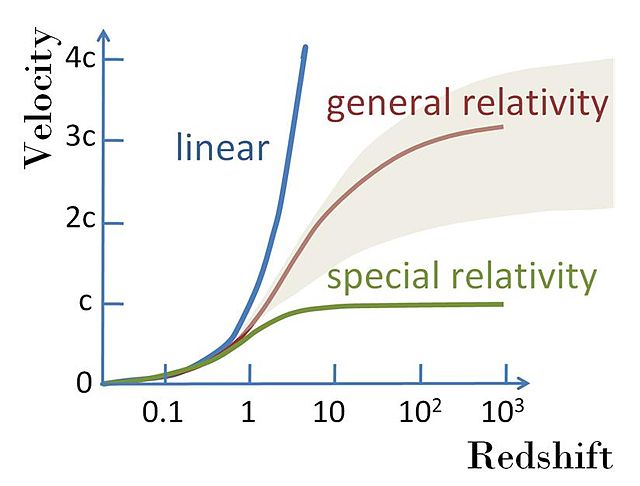
A variety of possible recessional velocity vs. redshift functions including the simple linear relation v = cz; a variety of possible shapes from theories related to general relativity; and a curve that does not permit speeds faster than light in accordance with special relativity. All curves are linear at low redshifts. See Davis and Lineweaver.
The landscape of H0 measurements around 2021, with the Planck (2018) and SH0ES (2020) values highlighted in pink and cyan respectively.
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation. The opposite change, a decrease in wavelength and increase in frequency and energy, is known as a blueshift, or negative redshift. The terms derive from the colours red and blue which form the extremes of the visible light spectrum. The main causes of electromagnetic redshift in astronomy and cosmology are the relative motions of radiation sources, which give rise to the relativistic Doppler effect, and gravitational potentials, which gravitationally redshift escaping radiation. All sufficiently distant light sources show cosmological redshift corresponding to recession speeds proportional to their distances from Earth, a fact known as Hubble's law that implies the universe is expanding.
High-redshift galaxy candidates in the Hubble Ultra Deep Field, 2012
Matter waves (protons, electrons, photons, etc.) falling into a gravity well become more energetic and undergo observer-independent blueshifting.