In geometry, the orientation, attitude, bearing, direction, or angular position of an object – such as a line, plane or rigid body – is part of the description of how it is placed in the space it occupies.
More specifically, it refers to the imaginary rotation that is needed to move the object from a reference placement to its current placement. A rotation may not be enough to reach the current placement, in which case it may be necessary to add an imaginary translation to change the object's position. The position and orientation together fully describe how the object is placed in space. The above-mentioned imaginary rotation and translation may be thought to occur in any order, as the orientation of an object does not change when it translates, and its position does not change when it rotates.
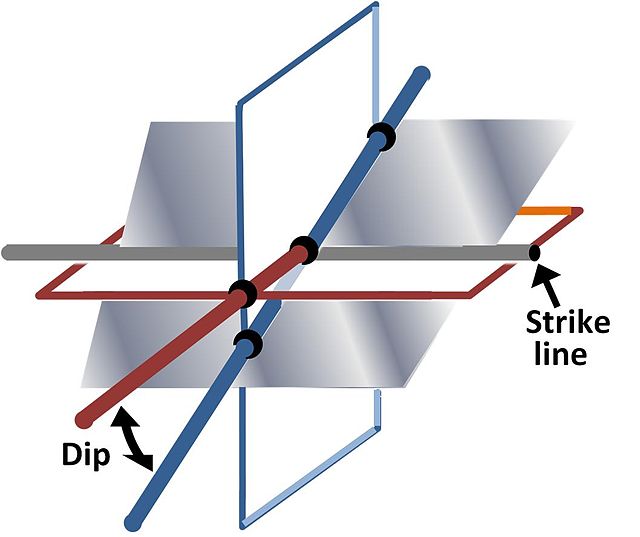
Strike line and dip of a plane describing attitude relative to a horizontal plane and a vertical plane perpendicular to the strike line
Rotation or rotational motion is the circular movement of an object around a central line, known as axis of rotation. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersecting anywhere inside or outside the figure at a center of rotation. A solid figure has an infinite number of possible axes and angles of rotation, including chaotic rotation, in contrast to rotation around a fixed axis.
Star trails caused by the Earth's rotation during the camera's long exposure time