A palace is a grand residence, often serving as a royal residence or the home for a head of state or some other high-ranking dignitary, such as a bishop or archbishop. The word is derived from the Latin name palātium, for Palatine Hill in Rome which housed the Imperial residences.
The Winter Palace, an imperial palace in Saint Petersburg, Russia; which served as the official residence of the Russian emperors.
The Royal Site of San Lorenzo de El Escorial, in Spain, is a Renaissance complex that has functioned as a royal palace, monastery, basilica, pantheon, library, museum, university and hospital.
The Blue House, the official residence of the president of South Korea
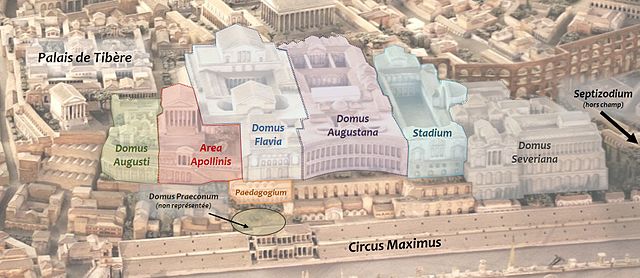
Domus Augustana of Palatine Hill in Rome, the origin of the term "palace"
The Palatine Hill, which relative to the seven hills of Rome is the centremost, is one of the most ancient parts of the city; it has been called "the first nucleus of the Roman Empire". The site is now mainly a large open-air museum whilst the Palatine Museum houses many finds from the excavations here and from other ancient Italian sites.
View of the Palatine Hill from across the Circus Maximus
Palaces on the Palatine
Palatine Hill from the Colosseum
Massive retaining walls extended the area on the Palatine available for the Imperial building complex.