In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
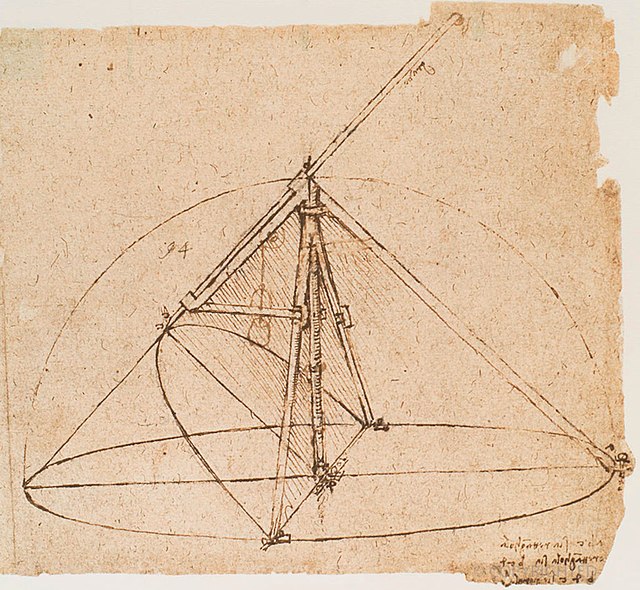
Parabolic compass designed by Leonardo da Vinci
A bouncing ball captured with a stroboscopic flash at 25 images per second. The ball becomes significantly non-spherical after each bounce, especially after the first. That, along with spin and air resistance, causes the curve swept out to deviate slightly from the expected perfect parabola.
Parabolic trajectories of water in a fountain.
The supporting cables of suspension bridges follow a curve that is intermediate between a parabola and a catenary.
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline.
This is the Ulam spiral, which illustrates the distribution of prime numbers. The dark diagonal lines in the spiral hint at the hypothesized approximate independence between being prime and being a value of a quadratic polynomial, a conjecture now known as Hardy and Littlewood's Conjecture F.
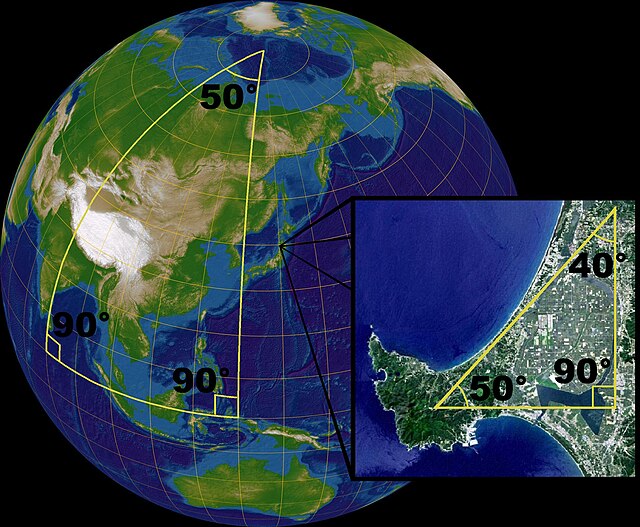
On the surface of a sphere, Euclidean geometry only applies as a local approximation. For larger scales the sum of the angles of a triangle is not equal to 180°.
The Babylonian mathematical tablet Plimpton 322, dated to 1800 BC
A page from al-Khwārizmī's Algebra