Rhombicosidodecahedron
Videos
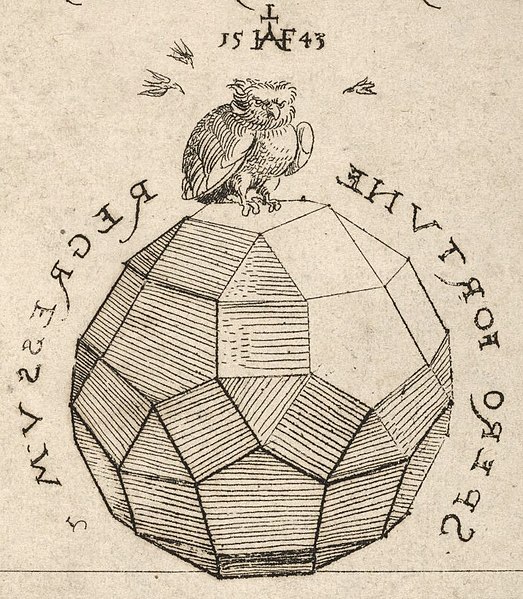
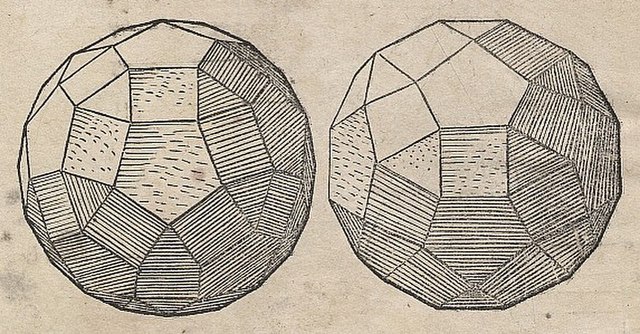
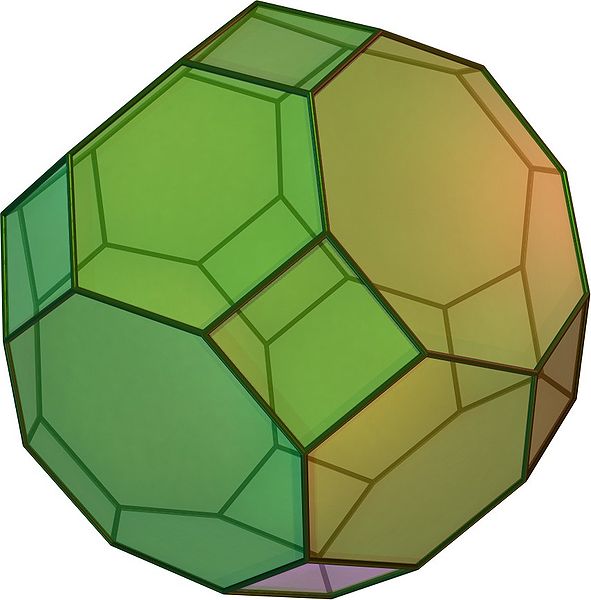
In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.
A version with golden rectangles is used as vertex element of the construction set Zometool.
Deltoidal hexecontahedron
Videos
In geometry, a deltoidal hexecontahedron is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian
Rhombicosidodecahedron
…angle 3-4: 159°05′41″ (159.09°) 4-5: 148°16′57″ (148.28°) References U27, C30, W14 Properties Semiregular convex Colored faces 3.4.5.4 (Vertex figure) Deltoidal hexecontahedron (dual polyhedron) Net In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed…
This figure from Perspectiva Corporum Regularium (1568) by Wenzel Jamnitzer can be seen as a deltoidal hexecontahedron.